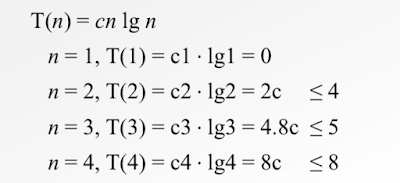- 컴퓨터 알고리즘 성능분석 (1)
- 컴퓨터 알고리즘 성능분석
- 정의 : 문제를 해결하기 위한 과정을 상세하게 단계적으로 표현한 것으로 입력과 출력으로 문제를 정의한다.
- 컴퓨터 알고리즘 단계
- 문제 정의 : 현실 세계의 문제를 컴퓨터를 이용해 풀 수 있도록 입력과 출력의 형태로 정의
- 알고리즘 설명 : 문제 해결을 위한 단계를 차례대로 설명
- 정확성 증명 : 항상 올바른 답을 내고 정상적으로 종료 되는지 증명
- 성능분석 : 수행 시간이나 사용 공간에 대한 알고리즘의 성능을 비교하기 위한 분석
- 컴퓨터 알고리즘 성능분석
- 특정 기계에서 수행 시간을 측정하는 방법은 현실적으로 불가능하고, 절대적 시간을 측정하여 비교하는 방법은 공정한 비교가 불가능하기 때문에 점근적 표기법을 사용한다.
- 점근적 표기법(Asymptotic notations)
- O-notation(빅오 표기)
- O(g(n)) = {f(n): n ≥ n0 인 모든 n에 대해 0 ≤ f(n) ≤ cg(n) 를 만족하는 양수 상수 c 와 n0 가 존재}
- f(n)은 cg(n)에 같거나 아래에 있어 점근적 상한(asymptotic upper bound)이라 한다.
- 기준점보다 빨라지지 않는 것을 보장한다.
- Ω-notation(오메가 표기)
- Ω(g(n)) = {f(n): n ≥ n0 인 모든 n에 대해 0 ≤ cg(n) ≤ f(n)를 만족하는 양수 상수 c 와 n0 가 존재}.
- f(n)은 cg(n)에 같거나 위에 있어 점근적 하한(asymptotic lower bound)이라한다.
- 기준점보다 느려지지 않는 것을 보장한다.
- Θ-notation(쎄타 표기)
- Θ(g(n))={f(n) : n ≥ n0 인 모든 n에 대해 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) 을 만족하는 양수 상수 c1 , c2와 n0 가 존재}.
- f(n)은 c1g(n)과 c2g(n)에 같거나 그 사이에 있어 점근적 상한 및 하한(asymptotic tight bound)이라한다.
- 두개의 기준선 사이에 있다는 것을 보장한다.
- 대체법(Substitution Method)
- 재귀함수에 대한 성능분석에 대해서 Substitution Method, Recursion-tree Method(재귀 트리/재귀 함수), Master Method(마스터 함수)
- 마스터 함수는 각 함수에 대해서 점근적 표기를 적용해서 맞는지 확인한다. 해당 링크는 다음과 같다. (https://en.wikipedia.org/wiki/Master_theorem_(analysis_of_algorithms))
- 보통은 대체법을 통한 성능분석은 해답의 형태를 추측하며, 수학적 귀납법을 이용해서 추측한 해답이 맞음을 증명한다.
- 수학적 귀납법으로 결론이 나와있는 해답을 이용해서 찾아낸다.
- T(n) = 2T([n/2])+n 시간 복잡도를 증명
- 추측 : T(n) = O(nlog(n))
- 증명 : T(n) <= cnlog(n), 적절한 상수 c를 설정한다.
- T(n/2) <= c(n/2)log(n/2) 에 대해 성립하는지 증명
- 적절한 c 를 설정
- 학습정리
- 컴퓨터 알고리즘 성능평가 : 문제를 해결하기위한 알고리즘은 여러 종류가 있지만 적절한 것을 고르기 위해 성능 평가와 비교가 필요하며 이를 상대적으로 평가할 수 있는 점근적 표현법이 사용
- 대체법 : 재귀 알고리즘은 간단히 계산하기 쉽지 않기 때문에 추측을 통해 대체법을 이용하여 수학접 귀납법을 증명하는 방법으로 이용
- 컴퓨터 알고리즘 성능분석 (2)
- 컴퓨터 알고리즘 성능분석
- 재귀 함수에 대한 성능 분석을 위해서 재귀 트리를 이용할 때는 적절한 해답을 찾기 위해서 좋은 추측을 먼저한다.
- 좋은 추측은 대체법을 통해서 증명하고, 재귀 함수의 성능을 분석한다.
- 재귀 함수에 대한 성능 분석 방법
- 트리에서 각 노드는 각 하위 문제에 대한 비용을 표현한다.
- 트리에서 레벨에 속한 노드들의 합은 레벨의 총 비용을 표현한다.
- 트리의 각 레벨의 비용을 모두 더하면 재귀 트리 전체의 비용이 표현된다.
- T(n) = 3T([n/4] + Θ([n^2]) 예시
- T(n) = 3T([n/4] + Θ([n^2]) 에서 Θ([n^2]) 를 이차식의 최소로 변경하면, c[n^2] (c 는 c>1 보다 크다.)
- T(n) = 3T([n/4]) + Θ([n^2]) 는 T(n) = 3T([n/4]) + c([n^2]) 으로 변경
- T(n) = 3T([n/4]) + c(n^2) 에서 n/4 에 대해서 정의를 하면, T(n/4) = 3T([n/16]) + c([([n/4])^2]) 이 함수가 T(n) 으로 표현하면 같은 함수 3개가 필요하며, 갯수는 3배씩 늘어나고, n은 n/4배씩 증가하는 형태가 되는 아래 트리와 같다.
- 재귀 트리를 이용 시에 구해야하는 부분
- Subproblem size for a node at depth
- The number of nodes at depth
- The number of levels
- The number nodes at the last level
- 재귀 트리로 구해야하는 부분을 적용하면
- Subproblem size for a node at depth i : ([n/4^i]) 로 괄호 안에 n 이 어떻게 변경되는지에 대한 내용이다.
- The number of nodes at depth i : 3^i 로 각 루트의 자식 노드가 몇 개씩 늘어나는지에 대한 내용이다.
- The number of levels : log4(n) + 1 로 T(1) 이 될 때까지를 구하면 된다.
- The number noes at the last level : n^(log4(3)) 으로 위에서 구한 level 로 T(1) 이 되었을 때 갯수를 생각하면 된다.
- 위의 함수를 정리하면 T(n) = O([n^2]) 임이 되고, 이를 좋은 추측이라고 한다.
- 재귀 함수로 표현된 부분을 재귀 트리로 좋은 추측을 하는 것으로 이를 증명하는 과정이 필요하다.
- 재귀 함수를 재귀 트리를 이용해서 좋은 추측을 했다면, 이를 증명하기 위해서는 마스터 함수 중에서 한가지 경우를 이용하는 대체법으로 이를 증명한다.
- 대체법을 이용한 방법은 위 1장에서 시간 복잡도 증명하는 부분을 참고한다.
- 학습정리
- 재귀 트리를 이용한 추측과 성능 분석 : 재귀 함수의 성능 분석을 위해 재귀 트리를 그려 해답을 추측하고, 이를 대체법을 이용하여 증명한다.
- 확률분석 (1)
- Hiring Problem의 정의 : 지원자 중 가장 뛰어난 직원을 고용하려고 할 때, 최소의 비용을 계산하는 문제
- 지원자를 매일 1명씩 인터뷰
- 면접 후에 지원자 고용여부를 즉시 판단
- 지원자를 고용하면 기존의 직원은 해고
- 지원자를 인터뷰 할 때마다 인터뷰 비용 지불 : Ci
- 지원자를 고용할 때마다 고용 비용 지불 : Ch
- Hiring problem 의 Pseudo code
- Hiring problem 의 비용계산
- 인터뷰 비용 Ci 는 고용비용 Ch 에 비해 매우 낮다.
- 인터뷰 횟수는 n 번 -> 고정
- 고용 횟수는 m 번 -> 변동
- 고용 비용 m * Ch 를 최소로 만들면 전체 비용이 최소가 된다.
- 최악의 경우는 모든 인터뷰이를 고용하는 경우로 m = n 이고 비용은 m (Ci + Ch)
- 인터뷰를 받으러 오는 사람들이 뒤쪽으로 갈수록 점점 더 우수한 사람들인 경우로 오름차순으로 정렬된 경우라고 생각하자.
- 해당 경우는 발생할 수 있지만 확률이 매우 희박하다.
- n 명의 후보자들이 오름차순으로 정렬될 확률은 1/n
- 평균적인 경우는 확률적 분석이 필요하다. 다음 그림과 같다고 하자.
- Indicator Random Variables
- i 번째 인터뷰이가 고용되는 경우는 1 번째부터 i-1 번째 인터뷰이가 i 번째 인터뷰이보다 우수하지 않은 경우로 확률은 1/i 가 된다.
- 이를 식으로 나타내는 아래와 같다.
- Randomized Order
- 고용 문제에서 인터뷰이의 순서들은 무작위로 보이기는 하나, 무작위라고 보장하지는 못한다.
- 따라서 Indicator random variable 을 사용하기 위해서는 인터뷰이를 무작위 순서로 인터뷰를 하도록 만들어주어야 한다.
- Permute-BY-Sorting Pseudo code
- Randomize-In-Place Pseudo code
- 쉽게 생각해서 한정된 숫자가 있고, 이를 중복없이 랜덤하게 뽑는 방법을 생각하면, 전체 숫자를 임의로 섞은 배열에서 하나씩 꺼내는 방법으로 해결할 수 있다.
- 학습정리
- Hiring 문제를 이용한 확률분석 : 고용문제는 인터뷰비용과 고용비용을 최소로 하면서 가장 좋은 사람을 뽑는 방법으로 이 문제를 해결하기 위한 확률분석방법을 이해할 수 있다.
- Indicator Random Variables
- Randomized Order
- 확률분석 (2)
- Balls and Bins 문제를 이용한 확률분석
- Balls and Bins 문제 정의
- 특정 바구니에 얼마나 많은 공이 들어갔는가?
- b 개의 바구니가 있고 n 개의 공을 던졌을 때, 확률은 n/b
- 특정 바구니에 들어갈 확률을 p 라고 하면 실패할 확률은 q = 1 - p
- X 를 n 번 던졌을 때 성공할 횟수라고 하면, X 의 범위는 0 ~ n 이고, 확률은 이항분포(Binomial distribution) 을 따르며, 아래 그림과 같이 표현한다.
- 이항 분포를 이용해서 기대 값을 구하면 다음 그림과 같다.
- 특정 바구니에 공이 들어가려면 평균적으로 공을 몇 번 던져야 하는가?
- b 개의 바구니가 있고 n 개의 공을 던졌을 때 특정 바구니에 들어갈 확률은 p 라고 하면, 실패할 확률은 q = 1 - p
- X 를 k 번째 던졌을 때 특정 바구니에 들어가는 경우라고 하면 k 번을 던져서 공이 k-1 번 안 들어가고 1 번 들어간 경우는 아래 그림과 같다.
- 해당 경우를 기하분포(Geometric Distribution) 이라고 부르며 q < 1 을 만족할 때 기대 값은 다음과 그림과 같다.
- 결과적으로 기대 값을 만족하기 위해서는 b 번을 던져야 한다.
- 모든 바구니에 공이 들어가려면 공을 몇 번 던져야 하는가?
- 모든 바구니에 공이 들어가야 조건을 만족하기 위해서는 비어있는 바구니에 공이 들어가는 경우가 b 번 발생해야 한다.
- 결국 비어있는 바구니에 공이 들어가는 경우가 B 번 발생할 때까지 던져야하는 공의 수를 구하는 문제와 같다.
- 공을 던졌을 때 바구니에 들어갈 확률은 앞에서 구했듯이 1/b 이다.
- 첫번째 공은 b 개의 바구니가 모두 비어 있으므로 확률은 b/b 로 반드시 비어 있는 바구니에 들어간다.
- 두번째 공은 b-1 개의 바구니가 비었으므로 (b-1) / b 로 비어 있는 바구니에 들어간다. 단, 두번째 던진 공이 첫번째 공이 들어간 바구니에 들어가면 다시 공을 던진다. 그러므로 던지는 횟수는 정해지지 않은 상태이다.
- i-1 개의 바구니가 채워진 다음에 던지는 첫번째 공은 b-i+1 개의 바구니가 비어 있으므로 (b-i+1) / b 의 확률로 비어 있는 바구니에 들어간다. 이 때, 던지는 횟수는 정해지지 않은 상태로 임의로 ni 로 정한다.
- 기대 회수는 확률의 역수이므로 ni에 대한 기대값은 다음 그림과 같다.
- 기대값을 구하면 다음 그림과 같다.
- 학습 정리
- Balls and Bins 문제를 통해서 확률분석방법을 확인했다.
- Binomial Distribution(이항분포) 과 Geometric Distribution(기하분포) 에 대해 알아보았는데 확률분석의 결과가 일반적으로 생각하는 확률과 크게 다르지 않다.
- 동적계획법 (1)
- 문제 해결 방법
- Brute-Force Approach (무작위 대입 접근) : 문제가 해결이 될 때까지 접근해서 해결한다.
- Divide and Conquer Approach : 문제를 해결할 때 하위로 나누어서 하위부터 점점 합쳐서 해결하며, 하위는 독립성을 가진다. ex) 합병정렬
- Dynamic Programming Approach : 문제를 해결할 때 하위로 나누는 것에는 Divide and Conquer Apporach 와 동일하나 동적 프로그래밍은 하위와의 관계에서 서로 종속성을 가질 때 사용한다.
- Greedy Approach : 문제를 해결할 때 현재 문제에서 가장의 최선이 전체의 최선이라 생각하고 현재에서 가장 최선의 선택을 해서 해결한다. ex) 탐욕 알고리즘
- Dynamic Programming (동적 프로그래밍)
- 주어진 문제를 하위로 나누어서 해결
- 동적 프로그래밍과 Divide and conquer 와 비슷하지만 문제간의 관계가 다르다.
- 동적 프로그래밍은 하위 문제가 서로 종속성을 가질 때 사용한다.
- 동적 프로그래밍과 최적화 문제는 4단계로 이루어진다.
- 최적해에 대한 구조적 특징을 분석
- 최적해 값을 구하기 위한 재귀적 정의가 가능한지 확인
- 하위문제로부터 최적해의 값을 계산
- 계산된 값으로부터 최적해를 만듦
- 동적계획법과 Assembly Line Scheduling
- Assembly Line Scheduling 과정
- 공장 조립 계획의 구조를 분석한다.
- 재귀적인 구조로 정의할 수 있는지 확인한다.
- 가장 빠른 시간 계산한다.
- 가장 빠른 시간일 때의 경로 구하기
- 위 그림에서 최적의 경로를 찾는다.
- 학습정리
- Dynamic Programming : 문제해결방법으로 최적화 문제를 해결할 때 문제의 크기를 작게 나누어서 해답을 찾으며, 이 때 작은 문제들은 서로 연관성을 가짐, 동적 계획법을 적용하기 위해서는 최적해 구조와 재귀 구조를 가져야 한다.
- 동적 계획법과 Assembly Line Scheduling : 조립을 통해 제품이 완성될 때까지 여러 개의 과정과 여러 개의 라인이 존재할 때 최적의 조합을 찾아 가장 빠른 시간과 경로를 동적 계획법을 이용하여 해결한다.
- 동적계획법 (2)
- 동적 프로그램
- 동적 프로그래밍은 주어진 문제를 하위로 나누어서 해결한다.
- 동적 프로그래밍은 문제를 작은 문제로 쪼개서 푼다는 의미에서 divide and conquer 와 비슷하지만 문제간의 관계가 다르다. (divide and conquer 는 독립적이고, 동적 프로그래밍은 서로 종속적이다.)
- 동적 프로그래밍은 모든 하위 문제를 풀고 그 결과를 저장해 둔다.
- 저장되어 있던 결과는 다음 단계의 문제를 푸는데 사용한다.
- 동적 프로그래밍은 최적화 문제를 푸는데 쓰인다.
- Matric-Chain Muliplication
- Matrix A와 B의 곱
- Matrix A의 행의 숫자가 Matrix B의 열의 숫자가 같다면 곱셈이 가능하다.
- A가 p * q 이고 B가 q * r 이라면 AxB는 p * r
- Matrix 의 곱셈에서는 순서에 따라 곱셈의 횟수가 큰 차이가 발생한다.
- 문제를 푸는 방법
- Brunte-Force approach
- 모든 가능한 경우를 모두 계산하는 방법
- 각각의 경우에 대해서 곱셈의 횟수를 계산
- 가장 곱셈의 수가 적은 방법을 선택
- 단점은 모든 가능한 경우를 모두 계산하기 때문에 계산 횟수도 증가하고, 수행시간도 오래걸린다.
- Dynamic programming
- 최적해 구조
- 동적 프로그래밍을 위해서는 재귀 함수가 되는지를 확인한다. -> 하위 문제와 서로 종속성을 가져야하기 때문이다.
- 동적 프로그래밍으로 문제를 풀면 아래 그림과 같다.
- 수행시간
- 전체 시간 : O(n^2)
- 하위 문제 수행시간 : Θ(n^2)
- 각 하위 문제를 푸는 시간 : O(n)
- 공간사용 : Θ(n^2)
- 학습정리
- Matrix-Chain Multiplication
- 행렬의 곱은 그 순서에 따라 곱셈의 횟수가 달라지기 때문에 효율적으로 계산하기 위해서는 가장 최소인 경우를 찾아야 한다.
- 동적계획법을 이용하여 이를 해결하는 방법을 확인하였는데 동적 계획법은 하위 문제가 얼마나 자주 등장하는지와 이를 저장할지의 여부에 따라 좀 더 효율적으로 문제를 해결할 수 있다.
- Greedy Approach (1)
- 문제 해결 방법
- Brute-Force Approach (Brute-Force Search or Exhaustive Search)
- 모든 경우의 답을 구해보는 일반적인 방법이다.
- 답이 있다면 항상 답을 찾으며 구현이 쉽다.
- 경우의 수에 비례하여 시간이 증가한다. 즉, 문제의 크기가 커지면 그만큼의 해결하는 시간도 증가한다.
- 예를 들어서 주어진 숫자의 약수 구하기, 주어진 숫자의 배수 구하기
- Divide and Conquer Approach
- 문제의 크기를 작게 나누어서 문제를 쉽게 풀기 위한 방법이다.
- 문제의 크기는 두 개 이상으로 쪼개어지고 문제의 해답을 바로 구할 수 있을 정도가 될 때까지 문제를 계속 분할한다.
- 하위 문제들이 서로 독립적이라 하위 문제를 따로 저장하진 않는다.
- 예를 들어서 정렬 문제 중에 Merge Sort, Quick Sort
- Dynamic programming Approach
- 문제의 크기를 작게 나누어서 문제를 쉽게 풀기 위한 방법이다.
- 문제를 작게 나누는 것은 Divide and Conquer Approach 와 비슷하나 상위 문제와 하위 문제가 서로 종속적인 관계를 가지고 있어서 하위 문제를 저장했다가 동일한 문제가 나오면 재계산하지 않고 저장된 답을 사용할 수 있다.
- 예를 들어 피보나치 수열, Matric-Chain Muliplication
- Greedy Approach
- 현재 상황에서 최선의 답을 선택한다.
- 현재 상황에서는 최선이지만 전체에는 최선이라는 보장은 없다.
- 최적 부분 구조 조건을 만족하면 결과가 우수하다.
- 예를 들어 허프만 코드, 최소 신장 트리
- 학습 정리
- Greedy Approach의 이해
- 문제 해결방법으로 Brute-force, Divide and Conquer, Dynamic programming, Greedy Approach 가 있으며, Greedy Approach 는 현재 상황에서 최선의 답을 선택하지만, 전체에서 최선의 답이라고 보장은 못한다.
- Greedy Approach (2)
- Huffman code
- 데이터를 압축하고 해제하는데 널리 쓰이는 방법으로 유동 길이 코드를 효율적으로 설정하여 Encoding 과 Decoding 에 문제가 없으면서 크기를 최대한 줄이기 위해 사용한다.
- 고정 길이 코드(Fixed-length code)는 사용 공간이 고정된 크기를 사용하여 표현한다.
- 유동 길이 코드(Variable-length code)는 사용 공간을 고정 크기가 아닌 유동 크기로 사용하여 메모리를 사용하는 것을 줄일 수 있다.
- Huffman code and Greedy Approach
- Prefix 가 중복되지 않게 유동 길이 코드를 만들기 위해서는 모든 경우의 수를 계산하여 고를 수도 있지만, Greedy Approach 를 이용하여 가장 빈도수가 낮은 문자들을 합치면서 트리 구조를 생성하는 방법이다.
- 아래 그림은 유동 길이 코드를 Greedy Approach 로 해결하는 부분이다.
- 아래 그림은 유동 길이 코드를 Greedy Approach 로 해결하는 부분으로 트리 구조를 생성한다.
- 스트링 매칭 (1)
- String Matching 의 이해
- 정의 : 입력으로 텍스트 T와 패턴 P 가 주어졌을 때, T에 P가 존재하는지에 대한 해답을 구하는 문제
- 활용
- 비교를 통한 대상 찾기하는 모든 기능에서 활용
- 웹 검색 사이트에서 정보를 검색하는 경우
- 워드 프로세서에서 특정 단어를 찾는 경우
- DB 검색, DNA 정보 검색, 침입 탐지 등 다양한 분야에 활용
- 기본적인 방법
- 텍스트 T가 있고, 패턴 P가 있을 때, 텍스트 T를 기준으로 패턴 P가 맞는지 하나씩 비교하는 방식으로 다음 그림과 같이 한 칸씩 이동해서 비교를 한다.
- 단점은 하나하나 비교하기 때문에 시간이 오래 걸리며, 하지 않아도 될 비교까지 하게 된다.
- KMP 알고리즘
- 정의 : Knuth, Morris, Prett 가 발견한 알고리즘으로 각 앞글자를 따서 붙여 졌으며, 스트링 매칭에서 불필요한 비교를 하지 않도록 한다.
- KMP 알고리즘을 이해하기 전에 Prefix(접두사)와 Suffix(접미사)를 이해해야한다.
- Prefix는 글자의 앞부분부터 표시하는 것으로 예를 들어 banana 라는 글자를 Prefix 과정으로 하면, "b", "ba", ... , "banana"
- Suffix는 글자의 뒷부분부터 표시하는 것으로 예를 들어 banana 라는 글자를 Suffix 과정으로 하면, "a", "na", ... , "banana"
- pi 배열로 0~i 까지의 부분 문자열 중에서 prefix와 suffix 가 동일해지는 가장 긴 문자열의 길이 단, 이 때, prefix 가 0~i가지의 문자열과 같으면 안된다. 그림으로 이해하면 다음과 같다.
- prefix와 suffix가 패턴 내에서 동일한 부분이 있기 때문에 텍스트에 매칭 시에 그 부분을 활용해서 동일한 위치만큼 건너뛰면서 스트링 매칭작업을 실시한다.
- 위 그림에서 보면, 미스 매칭이 된 경우에 패턴 내에 동일한 prefix, suffix 만큼 건너뛰어서 매칭 여부를 확인하는 것을 볼 수 있다.
- 학습 정리
- String Matching 의 이해 : 텍스트 T와 패턴 P가 주어졌을 때, T에 P가 얼마나 매칭되는지의 횟수와 위치를 구하는 문제이다.
- KMP 알고리즘 : String Matching 시에 하나하나 모든 것을 비교하는데는 오랜 시간과 많은 비교 횟수가 필요하여 이를 최소화 하기 위해서 나온 알고리즘이다.
- 스트링 매칭 (2)
- Exact Matching : 주어진 텍스트 T에서 찾고자 하는 패턴 P(집합이다.)가 발생하는 횟수와 모든 지점을 찾는 문제 예) P = aba, T = bbabaxbabay 가 주어지면, 3군데 매칭이 되고, 3, 5, 8 군데에서 매칭이 된다.
- Approximate string matching : 주어진 텍스트 T에서 찾고자 하는 패턴 P의 일부를 찾아서 발생하는 횟수와 모든 지점을 찾는 문제
예) p = aba, T = bbabaxbabay 가 주어지면, p = ab*, a*a, *ba, a**, *b*, **a - Exact Set Matching : 주어진 텍스트 T에서 찾고자 하는 패턴 P(집합이다.)가 발생하는 횟수와 모든 지점을 찾는 문제 예) P = {aba, bb, ab}, T = bbabaxbabay 가 주어지면, P 집합과 매칭되는 것을 일일이 다 확인한다.
- Aho-Corasik 알고리즘
- Exact Set Matching 시에 사용되는 패턴 집합 P 에 해당하는 문자들을 트리로 구성을 하며, 이를 키워드 트리(Keyword Tree) 라고 한다.
- 예제 P = {potato, poetry, pottery, science, school} 로 트리로 구성된다.
- Output-link 와 Failure-link 로 구성된다.
- Output-link 는 아래 그림과 같다.
- Failure-link 는 아래 그림과 같다.
- 학습 정리
- Exact Set Matching : 텍스트 T와 패턴 P의 집합이 주어졌을 때, 패턴 P의 집합을 효율적으로 찾는 문제이다.
- Aho-Corasik 알고리즘 : Output-link와 Failure-link 를 적용한 키워드 트리를 이용하여 Exact set matching 문제를 선형 시간에 해결이 가능하다.
- 정수론 (1)
- 정의 : 수의 성질을 연구하는 분야로 나눗셈 정리, 페르마 정리, 소인수분해, 중국인 나머지 정리 등의 이론이 있으며, 수의 성질을 이용한 암호 알고리즘이 연구되고 있다.
- 암호는 특정인에게 비밀정보를 전달하는데 사용하는 방법이나 체계를 의미하며 대표적인 예로 공개 키 암호시스템이 있다.
- 공개 키 암호시스템
- 정의 : 공개 키와 개인 키를 사용하여 메시지의 암호화와 사용자의 인증을 수행할 수 있는 암호 시스템으로 대표적으로 RSA, ECC, DSS 등이 있다. Diffie와 Hellman 연구자가 1976년에 제안했고, 기존에 키를 1개만 사용하는 것의 한계를 느껴 2개의 키를 사용하여 암호화와 사용자 인증을 수행할 수 있도록 했다.
- RSA : 소인수분해가 숫자가 커지면 커질 수록 어렵다는 성질을 이용했다.
- ECC : 타원의 두 중심점을 찾기 어렵다는 성질을 이용했다.
- DSS : 이산 대수의 어렵다는 성질을 이용했다.
- 공개 키 암호 시스템은 아래 문제를 해결하기 위해서 개발
- 기존의 비밀키를 사용하는 시스템에서 키를 분배하는 문제를 해결
- 네트워크에서 부인방지를 막기 위해 전자 서명의 문제를 해결
- 공개 키 암호 시스템의 구성
- 평문 (M)과 암호문 (C)
- 공개 키(Pu)와 개인 키(Pr)
- 암호 알고리즘(Enc)과 복호 알고리즘(Dec)
- 공개 암호시스템의 특징
- Trap Door One-Way Function : 단일 방향 함수로 역함수를 계산하는 것은 거의 불가능하지만, 특정 정보를 알고 있으면 역함수를 계산할 수 있다는 것을 의미한다.
- 공개 암호 시스템의 조건
- 공개 키는 모든 사람이 필요하면 얻을 수 있도록 공개
- 개인 키는 사용자만 보관 / 사용
- 공개 키 - 개인 키는 쌍으로 만들어지고 사용
- 공개키로 암호화한 내용은 개인 키로 복호화
- 개인 키로 암호화한 내용은 공개 키로 복호화
- 암호화와 관련된 그림
- 전자 서명과 관련된 그림
- RSA 암호 알고리즘
- 대표적인 예로 공인인증서에 사용되는 암호 알고리즘으로 1977년 MIT에서 개발되어 현재까지 사용하는 암호 알고리즘이다. Rivest-Shamir-Adelman 연구자가 공동으로 개발했으며, 블록 단위로 암호를 수행하며 0과 n-1 사이의 정수를 평문과 암호문으로 사용하는 키의 크기는 2048bit (2^2048 수 사용) 이상이 일반적이다.
- 크기가 큰 수는 소인수분해가 어렵다는 수의 성질을 이용해서 암호화를 수행하며 보통 수의 크기는 2048bit 이상을 사용한다.
- 소인수분해는 주어진 숫자의 약수를 찾는 방법으로 알려진 소수들로 주어진 숫자로 나누어 보고 약수를 지수승의 형태로 표현한다.
- 난수를 생성하고 알려진 소수로 나누어 보는 방법을 이용하여 크기가 큰 소수들을 모두 찾기 위한 연구가 진행되고 있다.
- RSA 암호 알고리즘의 암호화 / 복호화 그림
- 학습 정리
- 정수론과 공개 키 암호 알고리즘 : 정수론은 수의 성질을 이용하는 연구 분야로 공개 키 암호 알고리즘은 키 분배문제와 전자 서명 문제를 해결하기 위해서 등장하였으며, 정수론의 성질을 이용했다.
- 관련된 문서 : http://index-of.co.uk/Cryptology/05.pdf
- 정수론 (2)
- RSA 와 Extended Euclid GCD
- 정수론 : 수의 성질을 연구하는 학문으로 나눗셈 정리, 페르마 정리, 소인수분해 등의 이론이 있으며, 수의 성질을 이용하여 암호 알고리즘을 연구하는데 사용된다.
- 역원의 계산 : N과 e가 주어졌을 때 Modular n에서 e에 대한 역원인 d를 구해야하는 경우 Extended Euclide's GCD 로 계산한다.
- 서로소와 역원의 계산에 대한 그림
- RSA 암호알고리즘의 계산에 대한 그림
- 학습정리
- RSA와 Extended Euclid GCD : 공개 키 암호 알고리즘인 RSA는 크기가 큰 수는 소인수분해가 어렵다는 수의 성질을 이용하며 Extended Euclid GCD 함수를 이용하여 공개 키와 개인 키를 생성한다.
- Flow Networks (1)
- Flow Networks 는 그래프를 기반으로 정의된다.
- 정의 : 방향성 그래프에서 각 간선이 용량(Capacity)과 흐름(Flow) 을 갖는 경우로 다음 그림과 같다.
- Flow Network 에서는 Capacity와 Flow 양이 다르기 때문에 최대 Flow 양은 상황에 따라 다를 수 있다.
- 방향성이 있는 그래프와 다르게 최단 경로가 아닌 최소로 흘러들어가는 양으로 경로에 표시하며, 최대로 많이 흘려 보낼 수 있는지를 구한다.
- 해당 그림에 대한 내용은 Oil Pipeline 이 대표적인 예이다.
- 학습 정리
- Flow Network
- 방향성 그래프에서 각 간선이 capacity와 flow를 가지는 경우로 도로, 순환, 전자회로, 파이프의 흐름 등을 표현한다.
- Maximum flow problem 은 그래프에서 최대 흐름의 양을 찾는 문제이다.
- Flow Networks (2)
- Ford - Fulkerson 알고리즘
- 정의 : Flow Network 에서 Maximum Flow 를 찾는 알고리즘으로 Greedy 방식을 적용한다.
- 문제 해결 알고리즘
- Brute-Force Approach (무작위 대입 접근) : 문제가 해결이 될 때까지 접근해서 해결한다.
- Divide and Conquer Approach : 문제를 해결할 때 하위로 나누어서 하위부터 점점 합쳐서 해결하며, 하위는 독립성을 가진다. ex) 합병정렬
- Dynamic Programming Approach : 문제를 해결할 때 하위로 나누는 것에는 Divide and Conquer Apporach 와 동일하나 동적 프로그래밍은 하위와의 관계에서 서로 종속성을 가질 때 사용한다.
- Greedy Approach : 문제를 해결할 때 현재 문제에서 가장의 최선이 전체의 최선이라 생각하고 현재에서 가장 최선의 선택을 해서 해결한다. ex) 탐욕 알고리즘
- Ford - Fulkerson Method 3가지 아이디어
- Residual Networks
- 각 경로에서 최대흐름을 전송하고 난 후, 여분의 Capacity 로 만든 네트워크
- Gf -> Residual Network
- Ef -> Residual Edge
- 그림으로 나타내면 아래와 같다.
- Augmenting Paths
- Residual Network Gf 가 주어졌을 때, 시작점부터 도착점까지의 단순 경로(Simple Path) 이다.
- 그림으로 나타내면 아래와 같다.
- Cuts of Flow Networks
- 시작점과 도착점 사이를 반으로 나누어서 생각한다.
- 그림으로 나타내면 아래와 같으면, 다음의 식을 만족한다.
- 위 세가지 과정을 거치게 되면, Psuedo Code 로 나타내면 아래와 같다.
- 학습정리
- Ford-Fulkerson
- Greedy 알고리즘으로 Flow Network 에서 Max, Flow 문제를 해결한다.
- Augmenting path와 Residual network 를 이용하여 여분의 경로를 찾고 흐름의 양을 계속 추가하는 과정을 반복한다.
- Amortized Analysis
- 정의 : 자료구조에서 하나의 Operation 을 수행할 때 필요한 시간을 전체 Operation 을 수행할 때의 평균 시간으로 바꾸어 놓는 것
- 목표 : 최악의 경우일 때, 각 Operation 의 평균 성능을 보장해준다.
| HIRE-ASSISTANT(n) best ← 0 for i ← 1 to n do interview candidate i if candidate i is better than candidate best then best ← i hire candidate i |
|---|
| 인터뷰 | 고용 | |
|---|---|---|
| 횟수 | n | m |
| 1회 비용 | Ci | Ch |
| 전체 비용 | n * Ci | m * Ch |
| PERMUTE-BY-SORTING(A) 1. n ← length[A] 2. for i ← 1 to n 3. do interview candidate i 4. sort A, using P as sort keys 5. return A |
|---|
| RANDOMIZE-IN-PLACE(A) 1. n ← length[A] 2. for i ← 1 to n 3. do swap A[i] ↔ A[RANDOM(i, n)] |
|---|
| for each edge (u, v) -> E [G] do f[u, v] = 0 f[v, u] = 0 while there exists a path p from s to t in the redual network Gf do Cf(p) = min{Cf(u, v) | (u, v) is in p} for each edge (u, v) in p do f[u, v] = f[u, v] + Cf(p) f[v, u] = -f[u, v] |
|---|