- 컴퓨터 알고리즘 개요 (1)
- 컴퓨터 알고리즘의 정의 : 어떤 문제를 컴퓨터가 해결할 수 있도록 해결 방법을 효율성 있게 단계적으로 처리할 수 있도록 한다.
- 컴퓨터 알고리즘의 의미
- 컴퓨터 언어 (Computer Language) : 컴퓨터와 대화하기 위해서 사용하는 언어 (C, C++, Java 등)
- 컴퓨터 알고리즘 (Computer Algorithm) : 컴퓨터를 이용하여 주어진 문제를 풀기 위한 방법이나 절차 (정렬 알고리즘, 해시 알고리즘, 최단 거리 알고리즘 등)
- 컴퓨터 프로그램(Computer Program) : 컴퓨터가 특정 작업을 수행하기 위해 짜여진 명령의 순서
- 컴퓨터 알고리즘을 설명하는 4단계
- 문제 정의 (Problem definition)
- 해결하고자 하는 문제는 무엇인가?
- 입력과 출력 형태로 정의될 수 있는가?
- 컴퓨터가 수행할 수 있는 형태로 전환이 가능한가?
- 알고리즘 설명 (Algorithm description)
- 컴퓨터가 수행할 내용을 하나씩 차례대로 정의한 과정
- 예) 라면을 끓이는 과정
- 냄비에 물을 500ml 넣고, 가스레인지에 올린다.
- 온도계로 물이 100도가 되면 라면과 스프를 넣는다.
- 3분정도 계속 끊인다.
- 불을 끈다.
- 라면을 식탁에 둔다.
- 라면을 먹는다.
- 정확성 증명 (Correctness proof)
- 과정대로 수행하면 출력으로 항상 올바른 답을 내보내는가?
- 잘못된 답을 내보내는 경우는 없는가?
- 올바른 출력을 내보내고 정상적으로 종료 되는가?
- 성능 분석 (Performance analysis)
- 수행 시간 (Running Time)
- 사용 공간 (Space consumption)
- 컴퓨터 알고리즘 개요 (2)
- 컴퓨터 알고리즘을 설명하기 위한 4단계
- 문제 정의 (Problem definition)
- 알고리즘 설명 (Algorithm description)
- 정확성 증명 (Correctness proof)
- 성능분석 (Performance analysis)
- 성능 분석
- 컴퓨터 알고리즘의 수행 시간 분석
- 특정 기계에서 수행 시간을 측정하는 것은 공정하지 않다.
- 조건이 동일한 특정 기계에서 모든 알고리즘의 수행시간을 측정하는 방법은 현실적으로 불가능하다.
- 따라서 수행 시간이 아닌 수행 연산의 횟수를 비교하는 방식으로 분석한다.
- 성능 분석의 비교 대상
- 산술 연산 (Arithmetic Calculation) : Add, Multiply, Exponent, Modular...
- 데이터 입출력 (Data Movement) : Copy, Move, Save, Load...
- 제어 연산 (Access Control) : If, While, Register...
- 성능 분석을 위한 점근적 표기법 (Asymptotic notation)
- 점근적 표기법을 사용하는 이유는 알고리즘의 성능 분석을 하는데 수행시간이 아닌 함수를 수행하는 횟수로 하기 때문이다.
- O-Notation (빅오 표기법)
- O(g(n)) = {f(n): n ≥ n0 인 모든 n에 대해 0 ≤ f(n) ≤ cg(n) 를 만족하는 양수 상수 c 와 n0 가 존재}
- f(n)은 cg(n)에 같거나 아래에 있어 점근적 상한(asymptotic upper bound)이라 한다.
- Ω-Notation (오메가 표기법)
- Ω(g(n)) = {f(n): n ≥ n0 인 모든 n에 대해 0 ≤ cg(n) ≤ f(n)를 만족하는 양수 상수 c 와 n0 가 존재}.
- f(n)은 cg(n)에 같거나 위에 있어 점근적 하한(asymptotic lower bound)이라한다.
- θ-Notation(세타 표기법)
- Θ(g(n))={f(n) : n ≥ n0 인 모든 n에 대해 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) 을 만족하는 양수 상수 c1 , c2와 n0 가 존재}.
- f(n)은 c1g(n)과 c2g(n)에 같거나 그 사이에 있어 점근적 상한 및 하한(asymptotic tight bound)이라한다.
- 점근적 표기법 관련 블로그 : https://blog.naver.com/shruddnr1/220901997484
- 정렬문제
- 알고리즘 설명 4단계
- 문제 정의 (Problem definition)
- 알고리즘 설명 (Algorithm description)
- 정확성 증명 (Correctness proof)
- 성능 분석 (Performance analysis)
- 정렬문제 (Sorting Problem) 정의
- 알고리즘 문제로 입력과 출력이 존재해야 한다.
- 입력 (Input) : n개의 숫자들의 배열 <a1, a2, ... an>
- 출력 (Output) : 입력된 숫자의 배열이 a1' <= a2' <= ... <= an' 조건을 만족하도록 다시 나열한 결과 <a1', a2', ... an'>
- 오름차순 (Increasing Order) : 점점 숫자가 커진다.
- 내림차순 (Decreasing Order) : 점점 숫자가 작아진다.
- 예제)
- Input : <5, 3, 2, 4, 1>
- Output : <1, 2, 3, 4, 5>
- 선택 정렬 알고리즘
- 선택정렬 (Selection sort)
- 정의 : 선택하여 정렬하는 알고리즘으로 선택 대상은 최소값 또는 최대값이다.
- 최소값 선택 정렬 (Min-Selection sort) : 가장 작은 값을 선택 (오름차순)
- 최대값 선택 정렬 (Max-Selection sort) : 가장 큰 값을 선택 (내림차순)
- 최소값 선택 정렬 (오름차순 정렬)
- 정렬되지 않은 숫자 중에서 가장 작은 숫자를 선택한다.
- 선택한 숫자를 정렬되지 않은 숫자들 중에 첫번째 숫자와 자리를 바꾸면 선택된 숫자는 정렬된 것이다.
- 모든 숫자를 옮길 때까지 위 1-2번 과정을 반복한다.
- 최대값 선택 정렬 (내림차순 정렬)
- 정렬되지 않은 숫자 중에서 가장 큰 숫자를 선택한다.
- 선택한 숫자를 정렬되지 않은 숫자들 중에 첫번째 숫자와 자리를 바꾸면 선택된 숫자는 정렬된 것이다.
- 모든 숫자를 옮길 때까지 위 1-2번 과정을 반복한다.
- 정확성 증명은 수학적 귀납법을 이용하며, i번째 선택한 숫자가 i번째로 작은(혹은 큰) 숫자인지를 증명한다.
- 성능분석
- 최고차 항을 θ로 표현
- 최선/최악의 경우 수행 시간 : θ(n^2)
- 최선/최악의 경우 공간 : θ(n)
- 입력받은 숫자들의 어떤 배열형태를 가지던 최선의 경우, 최악의 경우는 발생되지 않는다.
- 삽입 정렬 알고리즘
- 알고리즘 설명 4단계
- 문제정의 (Problem definition)
- 알고리즘 설명 (Algorithm description)
- 정확성 증명 (Correctness proof)
- 성능 분석 (Performance analysis)
- 정렬 문제 (Sorting Problem) 정의
- 입력 (Input) : n개의 숫자들의 배열 <a1, a2, .. an>
- 출력 (Output) : 입력된 숫자의 배열이 a1' <= a2' <= ... <= an' 조건을 만족하도록 다시 나열한 결과 <a1', a2', .. an'>
- 오름차순 (Increasing Order) : 점점 숫자가 커진다.
- 내림차순 (Decreasing Order) : 점점 숫자가 작아진다.
- 삽입정렬 알고리즘
- 삽입 정렬 (Insertion sort)
- 정의 : 삽입을 이용한 정렬 알고리즘으로 삽입은 Key 값을 정렬된 리스트에 조건이 맞는 위치에 삽입한다.
- 예) Key 값이 3이고, 정렬된 리스트가 <1, 2, 4, 5, 6> 이라면, Key를 알맞은 위치에 삽입한 배열로 <1, 2, 3, 4, 5, 6> 이 된다.
- 삽입 정렬은 Key 값을 하나씩 추가하면서 정렬한다.
- A[1...n]이 주어진 배열이라고 한다.
- 첫번째는 A[2]을 Key 값으로 조건이 맞는 값을 정렬된 배열 A[1]에 삽입한다.
- 두번째는 A[3]을 Key 값으로 조건이 맞는 값을 정렬된 배열 A[1..2]에 삽입한다.
- N-1 번째는 A[N]을 Key 값으로 조건이 맞는 값을 정렬된 배열 A[1..N-1]에 삽입한다.
- 위와 같이 배열 A에 원소를 하나씩 추가하면서 정렬한다.
- 삽입정렬의 Pseudo Code
- 삽입 정렬 성능 분석
- 삽입 정렬의 수행 시간 분석
- 각각에서 동작하고 있는 부분 분석
- for j = 2 to A.length : n-1 만큼 삽입을 반복한다.
- key = A[j] ~ A[i + 1] = key : A[j] 를 Key 값으로 A[1,..j-1] 배열에 삽입한다.
- while i > 0 and A[i] > key ~ i = i - 1 : A[j] 삽입할 부분을 찾는다.
- A[i + 1] = key : A[j] 를 삽입한다.
- 위 분석을 표로 수행시간을 분석한 결과입니다.
- tj : j에 대한 while loop의 수행횟수
- T(n) : 표의 cost 열과 times 열을 곱한 수의 합이다.
- 시그마(∑) 에 대한 블로그 : http://blog.naver.com/dalsapcho/20141141955
- 입력의 크기가 동일하더라도 입력의 수행시간은 최선의 경우, 최악의 경우, 평균의 경우로 나누어서 생각할 수 있다.
- 최선의 경우는 이미 정렬된 경우로 tj = 1 인 경우로 T(n) 을 계산한 최종의 값이 an+b 인 N에 대한 선형함수로 표현이 된다.
- 최악의 경우는 반대로 정렬되어 있는 경우로 tj = n 인 경우로 T(n) 을 계산한 최종 값이 an^2 + bn + c 인 N에 대한 2차 함수로 표현할 수 있다.
- 평균의 경우는 최선과 최악의 사이에 존재하므로 시간 복잡도는 θ(n^2) 이다.
- 공간 복잡도는 제자리 정렬을 하므로 추가 공간을 사용하지 않아서 θ(n) 이다.
- 합병정렬 알고리즘
- 알고리즘 설명 4단계
- 문제정의 (Problem definition)
- 알고리즘 설명 (Algorithm description)
- 정확성 증명 (Correctness proof)
- 성능 분석 (Performance analysis)
- 정렬 문제 (Sorting Problem) 정의
- 입력 (Input) : n개의 숫자들의 배열 <a1, a2, .. an>
- 출력 (Output) : 입력된 숫자의 배열이 a1' <= a2' <= ... <= an' 조건을 만족하도록 다시 나열한 결과 <a1', a2', .. an'>
- 오름차순 (Increasing Order) : 점점 숫자가 커진다.
- 내림차순 (Decreasing Order) : 점점 숫자가 작아진다.
- 합병정렬 알고리즘
- 합병 정렬 (Merge sort)
- 합병을 이용하는 정렬 알고리즘으로 두 개의 정렬된 배열을 정렬된 하나의 배열로 합병한다.
- 예) <2, 5, 6, 8>, <1, 3, 4, 7, 9> => <1, 2, 3, 4, 5, 6, 7, 8, 9>
- 합병 정렬의 과정
- 두 개의 배열은 이미 정렬이 된 상태라고 가정을 한다.
- 각 첫번째에 위치한 두 값을 확인하여 더 작은(또는 더 큰) 숫자를 정렬할 새로운 배열에 순차적으로 삽입을 한다.
- 새로운 배열에 삽입한 특정 배열에 있는 값은 그 배열에서 삭제한다.
- 위 1-3의 과정을 두 배열의 값이 모두 새로 정렬할 배열에 모두 삽입될 때까지 진행한다.
- 성능분석
- 합병정렬의 수행시간 : 두 개의 정렬된 배열의 길이를 각각 n1과 n2라고하면 수행시간은 θ(n1 + n2)이다.
- 주요함수 : Compare(비교), Move(이동)
- Comparison 횟수 <= Movement 횟수
- Movement 횟수는 n1 + n2
- Comparison 횟수는 n1 + n2 보다 작거나 같다.
- Comparison 횟수와 Movement 횟수를 더하면, Comparison 횟수 + Movement 횟수 <= 2(n1 + n2)
- 최종적으로 θ(n1 + n2)
- 합병 정렬의 핵심은 크기가 커서 풀기 어려운 하나의 문제를 크기가 작아서 풀기 쉬운 여러 개의 문제로 바꾸어서 푼다. => Divide-and-Conquer approach
- Divide-and-Conquer approach 어원은 프랑스, 스페인 등 유럽 국가에서 넓은 아프리카를 지배하기 위해서 전체를 통치하지 않고, 각 지역을 쪼개서 지배하니 전체를 지배할 때보다 더 쉬웠다는 것에서 유래가 되었다.
- Divide : n keys 들을 두 개의 n/2 keys로 나눈다.
- Conquer : 합병 정렬을 이용해서 두 개의 배열을 정렬한다.
- Combine : 두 개의 정렬을 하나로 합치는 과정이다.
- 합병정렬의 Pseudo Code
- 합병 정렬 수행 시간
- Divide : 배열을 나누는 과정으로 상수시간에 수행된다. => θ(1)
- Conquer : 두 개의 하위 배열의 문제를 푸는 과정 => 2T(n/2)
- Combine : θ(n) 시간에 두 개의 정렬된 배열을 하나로 합치는 과정 => θ(n)
- T(n) 은 n = 1 이면, θ(1) 가 되고, n > 1 이면, 2T(n/2) + θ(n) 식으로 변경 가능하다.
- 이 때 c 를 크기가 1인 문제로 푸는 시간으로 생각을 해서 위 식을 정리하면 T(n) 은 n = 1 이면, c 가 되고, n > 1 이면, 2T(n/2) + cn 이 된다.
- 재귀를 이용해서 풀게 되면 아래와 같이 된다.
- 계속 진행을 하게 되면 아래와 같이 된다.
- 재귀트리를 이용해서 수행시간을 구해보면 아래와 같이된다.
- 위를 바탕으로 수행시간을 계산하면 cn * log(n) + cn = θ(log(n)) 이 된다.
- 힙 정렬(Heap Sort) (1)
- 힙 구조
- 힙 구조의 특성을 이용한 정렬
- 수행시간은 합병정렬과 동일한 O(nlogn)
- 삽입정렬과 동일한 제자리 정렬(Sort in Place)
- 힙의 형태(The shape of a heap)
- 완전 이진 트리(Complete binary tree)에 가까운 형태
- 이진 트리(Binary tree)는 각 노드의 자식 수가 2이하인 경우
- 완전 이진 트리는 Root 노드부터 Leaf 노드까지 빠짐없이 채워져 있는 이진트리를 의미한다.
- 왼쪽부터 채워진 형태로 배열로 정렬했을 때 빈 부분이 발생하지 말아야한다.
- Leaf 노드가 왼쪽은 비워져있고 오른쪽만 채워진 구조는 완전 이진 트리의 형태가 되지 않는다.
- 힙 특성
- 힙 구조를 만족하는 2가지 힙이 존재
- 최대 힙 특성(Max-Heap Property)
- A[Parent(i)] >= A[i]
- 부모 노드의 값은 항상 자식 노드의 값보다 크다.
- 전체 트리의 Root 노드 값이 결론적으로 가장 큰 값을 가진다.
- 각 하위 트리 구조의 Root 노드가 가장 큰 값을 가진다.
- 최소 힙 특성(Min-Heap Property)
- A[Parent(i)] <= A[i]
- 자식 노드의 값은 항상 부모 노드의 값보다 크다.
- 전체 트리의 Root 노드 값이 결론적으로 가장 작은 값을 가진다.
- 각 하위 트리 구조의 Root 노드가 가장 작은 값을 가진다.
- 위 최대 힙 특성 노드의 그림의 반대의 경우로 볼 수 있다.
- 힙의 배열 저장 방식
- Root 노드는 배열의 첫 번째 A[1]에 저장한다.
- 각 노드들은 레벨별로 저장한다.
- 밑에 그림은 최대힙일 때를 가정해서 노드를 저장한 예제이다.
- 힙을 배열에 저장하면 다음과 같이 검색이 가능하다.
- PARENT(i) -> return [i/2]
- LEFT(i) -> return [2 * i]
- RIGHT(i) -> return [2 * i + 1]
- 힙 노드의 높이(Heap's height of Node)
- 노드의 높이는 현재 노드에서 Leaf 노드까지 내려갈 때 가장 단순하게 내려가는 가장 긴 경로에서(simple path) 거쳐야 하는 간선의 수이다.
- 위 그림에서 단순하게 내려가는 가장 긴 경로를 보면 Root 인 16->14->8->2 로 볼 수 있으며 여기서 거치는 간선의 수는 총 3개의 간선을 지나므로 위의 힙 노드의 높이는 "3" 이라고 할 수 있다. (16-14 : 1개, 14-8 : 1개, 8-2 : 1개 => 총 3개)
- Root 노드로부터 트리의 높이를 구하는 수행시간
- θ(log(n))
- Heap은 완전 이진 트리 구조를 가지기 때문에 각 레벨마다 노드의 수가 2배씩 증가하므로 높이는 θ(log(n))
- 풀이
- Root 의 노드 개수는 1개 (2^0), 1 단계의 노드의 개수는 2개 (2^1), 2 단계의 노드의 개수는 4개(2^2) ... h 단계의 노드의 개수는 2^h 개가 된다.
- n = 2 ^ h 가 되며, 높이 h = log(n)이 되므로 높이의 대한 노드의 탐색하는 횟수인 수행시간은 θ(log(n))이 된다.
- 힙 특성 관리(Maintaining the heap property)
- Max-Heapify : 노드가 입력으로 주어졌을 때 노드의 좌 우 하위 트리들은 max-heap 특성을 유지하지만 노드의 값이 하위 트리 값보다 작거나 같아서 max-heap 특성을 만족하지 않을 때 max-heap 특성이 유지되도록 바꾸는 연산
- 주어진 힙 구조가 아래와 같을 때, 처리 방법
- 주어진 노드의 값을 "흘려내리게" 해서 주어진 노드와 하위 트리가 max-heap 특성을 가질 수 있도록 변경
- 위 그림처럼 흘려내리기를 이용해서 max-heap이 유지 되도록 만들어준다.(해당 조건은 앞에 힙 특성을 참고로 그 형태를 만들어준다.)
- Max-Heapify 의 수행 시간, T(n)
- n을 하위 트리의 노드의 개수라고 할 때
- 노드의 값을 바꿀 때 수행시간 : θ(1)
- 힙의 높이 O(h) = O(log(n))
- 따라서 전체 수행시간은 위 둘을 곱한 값인 O(log(n))가 된다.
- 힙 정렬(Heap Sort) (2)
- 힙 구조 만들기 (Building a heap)
- Build Max Heap (Pseudo Code)
- 특정 배열을 이진트리로 표현하는 방법은 앞장에서 힙의 배열 저장 방식에서 넣은 것과 동일하게 진행한다.
- MAX-HEAPIFY(A, i)는 자식을 가지는 마지막 노드부터 시작한다.
- Root 노드 방향으로 거슬러 올라가면서 MAX-HEAPIFY(A, i)를 진행한다.
- Max-Heapify는 부모노드가 자식노드보다 모두 크고, 완전 이진트리의 형태를 가지도록 만들어준다.
- 수행시간 분석
- MAX-HEAPIFY를 한 번 호출할 때마다 O(log(n))
- MAX-HEAPIFY의 호출 횟수는 O(n)
- 따라서 전체 수행시간은 1, 2를 곱한 O(nlog(n))의 형태를 가진다.
- 최대값 추출(Extract-Max)
- Heap에서 가장 큰 값을 제거하고 Max-Heap 구조를 복원하는 연산으로 다음에 알아보는 힙 소트에서 자세하게 다룬다.
- 힙 소트(Heap Sort)
- 힙 소트의 과정
- 가장 마지막에 있는 Leaf 노드와 Root 노드의 자리를 바꾸어준다.
- 자리를 바꾼 후에 가장 마지막에 있는 Leaf 노드를 제거한다.
- Max-Heap 구조가 망가졌기 때문에 Build-Max-Heap 을 이용해서 Max-Heap 구조를 복구해준다.

- 위 그림에서 보면 먼저 1과 16을 바꾼 후에 16을 끊고 그 후에 다시 Build-Max-Heap 과정을 반복한다.
- 정렬을 할 때 이 과정을 모든 노드가 끊어질 때까지 하며, 마지막에는 가장 작은 값이 Root 로 남아서 결국 차례로 확인하면 오름차순으로 정렬하게 된다.
- 힙 소트의 Pseudo Code)
- 힙 소트의 수행 시간
- A[1..n]에 대해 BUILD_MAX-HEAP을 수행하는 시간 O(nlog(n))
- Extract-Max를 n번 반복
- 전체 수행시간은 O(nlog(n))
- 퀵 정렬(Quic Sort)
- Divide-and-Conquer paradigm을 사용
- Partition을 이용
- 하나의 기준 값인 Pivot element를 지정해서 그 값보다 작은 값은 왼쪽으로 그 값보다 큰 값은 오른쪽으로 위치하게 변경하는 방법이다.
- 위 그림처럼 임의의 값 Pivot element를 지정한 후에 작은 값은 왼쪽에 큰 값은 오른쪽에 위치하도록한다.
- 해당 내용은 오름차순일 경우에 해당하고, 내림차순의 경우는 반대로 진행한다.
- 퀵 정렬의 Pseudo Code
- 퀵 정렬의 수행시간
- 수행시간 분석
- Partition에 걸리는 시간 : θ(n)
- Partition의 횟수는 경우에 따라 횟수가 달라지는데 Balanced partitioning 일 때와 unbalanced partitioning 두 가지 경우로 나뉜다.
- Balanced partitioning
- 각 하위 문제의 크기가 기존 문제의 크기의 절반 정도인 [n/2]와 [n/2]-1이 되도록 나누어지는 경우이다.
- T(n) <= 2T(n/2) + θ(n) = O(nlong(n))
- 풀이를 하면 다음 그림과 같이된다.
- Unbalanced partitioning
- 형태는 다음 그림과 같이된다.
- 위 그림을 풀이하면 다음 그림과 같이 된다.
- 선형 시간 정렬 알고리즘
- 비교 정렬의 하한 값
- Heap sort, Merge sort, Insertion sort, Selection sort, Quick sort는 모두 비교 정렬로 각 숫자를 비교해서 크거나 작은 순으로 정렬하도록 했다.
- 비교 정렬의 하한값(Lower bounds)
- 하한 값은 오메가를 이용해서 수행시간을 분석하게 된다. (2. 컴퓨터 알고리즘의 개요(2)에서 성능분석 부분에서 다루었다.)
- 위 표에서 보면, 비교 정렬이 아무리 빨라도 평균적으로 Ω(n lg n) 보다는 느리다.
- 계수정렬 알고리즘
- 계수 정렬(Counting sort)
- 무엇을 정렬하는 데 이용하는가?
- 계수를 이용하여 정렬하고, 실제 숫자를 세는 방법으로 숫자가 몇 개인지를 기록한다.
- 임의의 숫자 x에 대해서 입력이 되었으면 x보다 작은 원소의 개수가 i-1개라면, 정렬 후에 x의 위치는 i 번째에 위치해야한다. -> x보다 작은 원소의 개수는 원소의 개수를 세어서 확인할 수 있다.
- 원래 숫자가 있는 배열이 있고, 최소값과 최대값을 통해서 각 숫자가 원래 배열에 몇 개씩 있는지를 세어서 기록하는 카운트 배열을 만든다.
- 위 가정대로 x보다 작은 원소의 개수가 i-1개이면, x보다 작은 숫자들이 i-1 번째까지 모두 정렬되고 x가 들어가야 할 자리가 i 번째가 된다는 정의에서 계수 정렬을 시작한다.
- 위 그림에서보면 원래 배열은 A가 되고, 카운트 배열이 C가 되고, 정렬된 후의 배열이 B가 된다.(별도의 과정은 생략한다.)
- 카운트 배열을 누적해서도 구할 수 있는데 이는 그 숫자가 들어가야할 인덱스 값과 일치하게 된다. 아래 그림은 해당 과정이다.
- 다음은 계수 알고리즘의 수행시간을 계산하기 위한 그림이다.
- 전체 수행시간을 구하기 위해서는 위 각 수를 더해야 하고, 결과는 Θ(k+n) 이 된다.
- 전체 수행시간을 보면 k는 입력되는 정수의 범위이고, 만약, k = O(n) 이라면, 수행시간은 Θ(n)이 된다.
- 기수 정렬 (Radix sort)
- 기수 정렬은 각 자리수를 비교해서 각 자리 수에 맞게 정렬하는 방법이다.
- 세 자리의 숫자를 기수 정렬로 동작 시키면, 세번째 자리들끼리 비교해서 정렬하고 두번째 자리들끼리 비교해서 정렬하고 첫번째 자리들끼리 비교하면 모두 정렬이 된다.
- 기수 정렬의 예 (MSB -> LSB)
- 기수 정렬의 예 (MSB <- LSB)
- 기수 정렬의 Pseudo Code
RADIX-SORT(A, d)
1. for i = 1 to d
2. use a stable sort to sort array A on digit i - 기수 정렬의 수행 시간은 Θ(d(n + k))
- d 자리 수 숫자 n개가 주어졌을 때 각 자리 수에서 최대 k 값을 가질 수 있다고 가정
- d 가 상수이고 k = O(n)이므로 기수 정렬은 선형 시간에 수행된다.
- 해쉬 알고리즘 (1)
- Direct-address table
- 크기가 |U| 인 테이블 T를 생성하고 key k를 slot k에 저장하는 방식
- 중복되는 key는 없다고 가정한다.
- Direct-address table을 그림으로 보면 다음과 같다.
- 성능분석
- Direct-address tables의 주요함수
- 각각의 수행시간은 O(1)로 상수 횟수만큼의 수행시간이 걸린다.
- Direct-address의 공간 복잡도
- Θ(|U|)
- 실제 공간 사용을 전체 공간으로 나눈 |K|/|U|를 적재율이라고 한다.
- 적재율은 전체에서 현재 사용하고 있는 공간의 비율정도로 생각하면 된다.
- 만약 적재율이 낮다면, 실제로 대부분의 공간이 사용하지 않고 빈 공간으로 남아 있기 때문에 공간이 낭비된다.
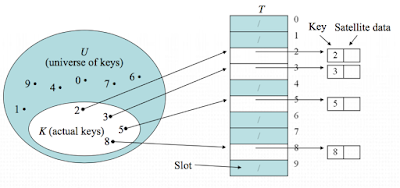
- 해슁(Hashing)
- Direct-address table에서 적재율이 낮으면, 빈 공간이 많이 발생해서 낭비가 되기 때문에 조금 더 효율적으로 쓰기 위해서 해슁이 등장하였다.
- Key k를 저장할 때 slot k에 저장하는 것이 아니라 slot h(k)에 저장한다.
- 이것을 key k가 slot h(k)로 해쉬되었다고 하며, h(k)를 key k의 해쉬 값이라고 부른다.
- 이 때 h()를 해쉬 함수(hash function)라고 부른다.
- h : U -> {0, 1, ... , m-1}
- 이렇게 구성한 테이블을 해쉬 테이블(hash table)이라고 한다.
- Hash Table을 그림으로 보면 다음과 같다.
- 성능분석
- 수행시간 분석
- Insertion : O(1)
- Deletion : O(1)
- Search: O(l) -> 이 때 slot은 항상 비어져 있으며 이중 연결리스트로 구현되어 있다고 가정하며 리스트의 길이를 l 이라고 생각한다.
- 충돌문제 (Collision)
- 두 개의 key가 동일한 hash 값을 갖는 경우 "충돌이 발생했다." 라고 한다.
- hash를 사용하면서 충돌이 아예 발생할 수 있는 방법은 없으며, 충돌이 적은 좋은 해쉬 함수를 쓰는 것이 방법이다.
- 하지만 테이블의 크기가 해쉬 함수의 치역 영역보다 크다면 |U|>m 충돌을 피하는 것은 매우 어렵니다.
- 체인을 이용한 충돌해결법 (Collision resolution by chaning)
- 중복되는 key 값이 있을 경우, 해당 슬롯을 연결리스트로 저장한다.
- 다음 해당 부분을 그림으로 나타낸 것이다.
- 주요 함수
- 최악의 경우의 수행시간 (Worst Case)
- Θ(n)
- 모든 key 값 k가 하나의 slot으로 해슁되는 경우는 길이가 n인 이중 연결 리스트가 생성된다.
- 해쉬 테이블이 아닌 일반적인 리스트에 저장하는 것과 성능이 동일하다.
- 평균적인 수행시간 (Average Case)
- Θ(1+a)
- 이 때 a는 적재율(load factor)이라고 부르며 a = n/m으로 계산한다. -> Θ(1+(n/m)) 으로 바꿀 수 있다.
- n은 테이블의 원소 개수이고, m은 slot의 수이다.
- 좋은 해쉬함수는 무엇인가? 중복되는 값이 없고 각 해쉬 함수의 값이 골고루 나오는 것이다.
- 좋은 해쉬함수는 simple uniform hashing을 만족하는 해쉬 함수이다.
- 각각의 key는 중복없이 m개의 slot으로 동일한 확률로 해쉬된다.(Simple)
- 각각의 key는 다른 key값의 해쉬값과 관계엾이 해쉬된다.(Uniformly)
- m개의 slot이 있으면 중복 없이 확률적으로 m개의 slot에 골고루 나누어지는 것이 좋으며 이것을 simple uniform hashing이라고 부른다.
- 효율적인 해쉬 값의 선택방법
- 2^p에 너무 가깝지 않은 소수를 선택하는 것이 충돌을 방지하는데 도움이된다.
- 2^p인 경우는 해쉬함수가 하위 p비트가 되는데 해쉬함수가 key 값 전체에 따라 바뀌지 않고 하위 p 비트에만 영향을 주어 충돌확률이 높아진다.
- 2^p-1 도 위와 동일한 이유에서 충돌확률이 높아진다.
- 해쉬 알고리즘 (2)
- Open-Addressing 개요
- Hash Table이 충돌 발생을 피할 수 없으며, 이 때 충돌이 발샐할 때마다 선형 리스트로 저장되어 저장공간을 차지 않도록 하는 방법이 필요하여 나온 방법이 Open-Addressing 이다.
- Open-Addressing 이란? 충돌(Collision)을 피하기 위한 다른 방법으로 key를 hash table에 직접 저장한다.
- 장점
- 포인터를 사용하지 않아도 되므로 구현이 간편한다.
- 포인터를 사용하지 않으므로 추가 메모리 공간 사용이 가능하다.
- 공간의 충돌 문제가 줄어들며 자료 검색이 미세하게 빨라진다.
- Open-Addressing의 종류 : 선형 프로빙(Linear probing), 이차식 프로빙(Quadratic probing), 이중 해싱(Double hashing)
- 선형 프로빙 (Linear probing)
- 삽입 연산 (Insertion)
- 빈 slot이 나올 때까지 해쉬 테이블을 탐색
- Key가 삽입되는 형태에 따라서 빈 slot의 위치가 결정
- 모든 Key 값에 대해 탐색 순서는 <0, 1, ... , m-1>에 대해 <h(k, 0), h(k, 1), ... , h(k, m-1)>을 탐색한다.
- 해쉬 삽입 (HASH-INSERT)의 Pseudo code
- 해쉬 검색 (HASH-SEARCH)의 Pseudo code
- 해쉬삭제 (HASH-DELETION)
- 삭제는 실제로 key 값을 삭제하는 것이 맞을까?
- 삭제를 위해서 먼저 해쉬 검색을 진행하게 된다.
- 빈 slot이 있는 경우, 원래 값이 있었는데 지워서 비어 있는지 아니면 원래 값이 없어서 빈 slot인지를 구분할 수 없기 때문이다.
- 실제로 값을 지우게 될 경우, 해쉬 검색을 할 때 반복의 끝나는 조건이 비어 있는 값이면 해쉬검색을 멈추게 되기 때문에 다음에 데이터가 있어도 해쉬 검색을 멈추게 되어 빈 값 이후에 값 들에 대해서는 검색을 할 수 가 없다. (until T [ j] == NIL or i == m) => NIL은 빈 값을 의미한다.
- 실제로 값을 지우는 경우는 "DELETED" 라고 표시한다.
- Open-Addressing 기술
- Open-Addressing 기술
- 선형 프로빙 (Linear probing)
- 이차식 프로빙 (Quadratic probing)
- 이중 해싱 (Double hashing)
- 선형 프로빙 (Linear probing)
- 일반적인 해쉬 함수 h' : U -> {0, 1, ... ,m-1}가 주어졌을 때 보조 해쉬 함수 (auxiliary hash function)을 사용해서 선형 프로빙을 하는 방식
=> h(k, i) = (h'(k) + i) mod m (i 는 충돌이 발생하면 1씩 증가한다.) - 선형적인 형태로 충돌이 발생하면 1씩 증가하면서 빈 slot을 찾는 작업을 반복한다.
- 선형 프로빙의 장점과 단점
- 구현은 매우 쉬우나 primary clustering문제가 있다.
- primary clustering 이란? 충돌이 발생하면 그 주변으로만 데이터 들이 뭉쳐서 테이블을 구성하는 현상을 말한다.
- 값이 들어있는 slot의 수가 많으면 평균 검색시간이 증가한다.
- key 값을 넣을 빈 slot은 뭉쳐있는 slot들의 끝부분에 존재하기 때문에 들어있는 slot들이 뭉쳐있는 경우가 많다.
- 선형 프로빙의 예) i 는 충돌 횟수로 발생할 때마다 1씩 증가한다.
- 이차식 프로빙(Quadratic probing)
- 이차식 프로빙은 다음과 같은 형태의 해쉬함수를 사용한다.
=> h(k, i) = (h'(k)+c1*i+c2*i^2) mod m - 이 때 h'은 보조 해쉬 함수이고 c1과 c2는 0이 아닌 상수이다.
- 즉, 주어진 Hash함수 외에 i 에 대한 2차함수꼴로 slot을 이동하면서 빈 slot을 찾는다.
- 이차식 프로빙의 단점
- 만약 두 key의 처음 probe 값이 동일하다면 빈 slot을 찾는 과정이 동일하므로 같은 slot을 탐색한다.
- 이유는 h(k1, 0) = h(k2, 0)이면, h(k1, i) = h(k2, i) 이기 때문이다.
- 이런 특성을 secondary clustering 이라고 부
- 처음 충돌한 위치가 같다면 다음 충돌할 위치에서도 반복적으로 계속 충돌이 나게 된다. (처음 시작 값이 같으면 매번 계산할 때마다 이전의 key 값과 동일한 위치만큼 이동하기 때문이다.)
- 이차식 프로빙의 예) i 는 충돌 횟수로 발생할 때마다 1씩 증가한다.
- 이중해싱(Double hashing)
- 이중 해싱은 다음과 같은 형태의 해쉬 함수를 사용한다.
=> h(k, i) = (h1(k) + i * h2(k)) mod m - 처음 탐색하는 위치가 T[h1(k)]이다.
- 그 다음부터는 h2(k) modulo m 만큼 이동하면서 탐색한다.
- 충돌이 발생했을 때, 이동하는 거리가 hash함수에 의해 계산되어 무작위로 빈 slot을 찾게한다.
- 이중해싱의 주의점 및 함수 구성 방법
- h2(k)함수는 해쉬 테이블의 크기 m과 서로 소 관계여야 한다.
- 이것을 만족하는 가장 쉬운 방법은 m을 2의 지수승으로 두고 h2가 항상 홀수가 되도록 만드는 것이다.
- 다른 방법은 m을 소수로 하고 h2을 m보다 작은 양수로 정하는 것이다.
- 자칫 잘못 지정하게 되면, 충돌이 발생하면 동일한 위치에서만 계속 검색을 하게 되어서 삽입이 끝나지 않을 수도 있다.
- 이중해싱의 예) i 는 충돌 횟수로 발생할 때마다 1씩 증가한다.
- 그래프의 기초
- 그래프 기초(Graph Basics)
- 정의 : 그래프 G는 (V, E)의 쌍이다.
- 이 때 V는 정점(vertex)의 집합(set)이고 E는 간선(edge)의 집합이다.
- 정점은 독릭된 개체로 동그라미로 표현한다.
- 간선은 두 정점을 잇는 개체로 직선이나 화살표가 있는 선으로 표현한다.
- 그래프의 종류
- 방향성 그래프(Directed graph)
- 방향성이 있는 간선을 가지고 있는 그래프이다.
- 정점 V = {1, 2, 3, 4, 5, 6}
- 간선 E = {(1,2), (2,2), (2,4), (2,5), (4,1), (4,5), (5,4), (6,3)}
- 방향성 그래프에서 두 개의 정점에 대해서 최대 2개의 간선이 존재한다.
- 강한 연결 (Strongly connected): 방향성 그래프에서 정점의 각 쌍이 서로 도달 가능하다면 강하게 연결되어 있다고 한다. (V = {(4, 5), (5, 4)} 는 각 쌍이 도달가능하므로 강한 연결이라고 한다.)
- 강한 연결 요소(Strongly connected components) : 방향성 그래프에서 최대한 많은 정점을 강하게 연결한 하위 그래프
- 간선의 개수 : |E| <= |V|^2
- 무방향성 그래프(An undirected graph)
- 방향성이 없는 간선을 가지고 있는 그래프이다.
- 간선이 방향이 없으므로 직선을 사용한다.
- 간선 (a, b)와 간선 (b, a)는 같다.
- 간선의 개수 : |E| <= |V| * (|V|-1) / 2
- 인접(Adjacency)
- (u, v)라는 간선이 있다면, 정점 u 와 정점 v 가 '인접하다' 고 한다.
- 무방향성 그래프에서는 인접관계는 동일하다.
- 방향성 그래프는 방향이 있기 때문에 인접관계는 동일하지 않다.
- 차수(Degree)
- 방향성 그래프의 차수
- 방향성 그래프의 차수에는 진출차수(out-degree)와 진입차수(in-degree)가 있다.
- 진출차수(out-degree)는 정점을 나가는 간선의 수이다.
- 진입차수(in-degree)정점으로 들어오는 간선의 수이다.
- 그래프의 차수는 진입차수와 진출차수의 합이다.
(degree = out-degree + in-degree) - 무방향성 그래프의 차수
- 무방향성 그래프에서 진입차수와 진출차수는 방향성이 없기 때문에 정의할 수 없으며, 차수만 정의할 수 있다.
- 무방향성 그래프에서의 차수는 정점에 연결된 선의 개수이다.
- 경로(Path)
- 정점 u 로 부터 정점 v 까지의 경로로, 정점의 순서이다.
- 정점의 순서가 <V0, V1, V2, ... , Vk> 라고 할 때 V0 = u, Vk = v 가 되며, 각 Vi+1 은 Vi 에 인접한 경우이다.
- 경로의 길이(length)는 경로에 있는 간선의 수이다.
- 정점 u 에서 정점 v 까지 경로가 있다면, v 가 u 에서 도달 가능하다고 한다.
- 단순경로 (Simple path) : 경로에 있는 모든 정점들이 서로 다른 경우이다.
- 경로 <1, 2, 4, 5> 는 단순경로의 조건을 만족하여 단순경로라고 한다.
- 경로 <1, 2, 4, 1, 2> 는 경로 사이에 같은 정점이 있기 때문에 단순경로라고 하지 않는다.
- 순환과 단일 순환(Cycle and simple cycle)
- 순환 : 경로 <V0, V1, ... , Vk> 에서 V0 = Vk 라면 순환이 된다.
- 단일 순환 : 순환 <V0, V1, ... , Vk>에서 V0, V1, ... , Vk 가 서로 다르면 단일 순환이라고 한다.
- 비순환 그래프 (An acycle graph) : 순환이 없는 그래프
- 연결 그래프(A connected graph) : 정점의 모든 쌍이 경로를 가지는 무방향성 그래프
- 연결 요소(Connected components) : 무방향성 그래프에서 정점들이 최대한 연결되어 있는 하위 그래프
- 무방향성 그래프와 방향성 그래프의 변환
- 방향성 또는 무방향성 그래프를 반대의 그래프로 바꾼 후에 다시 원래대로 바꾸었을 때 같은지 여부로 확인 가능하다.
- 무방향성 그래프 -> 방향성 그래프 -> 무방향성 그래프로는 가능하다.
- 방향성 그래프 -> 무방향성 그래프 -> 방향성 그래프로는 가능하지 않다.
- 완전 그래프(A complete graph)
- 정의 : 무방향성 그래프에서 모든 정점의 쌍이 서로 인접하는 경우이다.
- 완전 그래프의 종류
- 포레스트(Forest) : 순환하지 않는 무방향성 그래프
- 트리(Tree)
- 포레스트가 연결되어 있는 경우
- 연결된 비순환 무방향성 그래프(Connected, Acyclic, Undirected Graph)
- 그래프의 표현
- 인접리스트 표현 (Adjacency-list representation)
- 정점 하나당 리스트 하나인 크기가 |V|인 배열
- 정점 하나에 인접한 모든 정점을 리스트에 저장
- 방향성 그래프는 아래 그림과 같이 표현한다.
- 무방향성 그래프는 방향성 그래프로 변환해서 저장하며 아래 그림과 같이 표현한다.
- 공간은 Θ(V + E) 만큼 차지한다.
- 인접행렬 표현 (Adjacency-matrix representation)
- 크기가 |V| x |V|인 행렬
- 두 정점 i 와 j 를 잇는 간선이 있다면 행렬의 (i, j)는 1, 아니면, 0 이다.
- 방향성 그래프는 아래와 같이 표현한다.
- 무방향성 그래프는 아래와 같이 표현한다.
- 무방향성 그래프는 양방향으로 간선이 존재하므로 상, 하위 삼각 행렬로 대칭된다.(Lower traingular matrix)
- 공간은 Θ(V^2) 만큼 차지한다.
- 인접 리스트와 인접 행렬의 비교
- 저장 공간
- G의 사이가 벌어져 있다면, 인접 리스트가 낫다. -> |E| <= |V|^2
- G가 촘촘하면, 인접 행렬이 낫다. -> 행렬은 1 비트만 사용
- 간선을 찾는데 걸리는 시간
- 인접 리스트 : O(V) time
- 인접 행렬 : Θ(1) time
- 모든 간선을 찾거나 방문하는데 걸리는 시간
- 인접 리스트 : Θ(V + E)
- 인접 행렬 : Θ(V^2)
- 가중 그래프 (Weighted graph)
- 정의 : 간선이 숫자로 표현되는 값을 가지는 그래프
- 인접 리스트에서 가중 그래프 표현
- 인접 행렬에서 가중 그래프 표현
- 넓이 우선 탐색 (Breadth-first search)
- 트리 탐색하는 방법 중에 하나이다.
- 거리 (Distance)
- 정점 u 부터 정점 v 까지의 거리
- 정점 u 부터 정점 v 까지의 최단 경로(shortest path)에 있는 간선의 수 거리
- 그래프 G = (V, E) 와 시작점 (Source) s 가 주어졌을 때, s 에서 도달 가능한 모든 간선을 탐색하여 찾는 과정
- 시작점으로 부터 거리를 하나씩 늘려가면서 정점을 발견한다.
- 시작점 s 로 부터 1 떨어져 있는 노드들을 탐색하면 아래 그림과 같다.
- 시작점 s 로 부터 2 떨어져 있는 노드들을 탐색하면 아래 그림과 같다.
- 시작점 s 로 부터 3 떨어져 있는 노드들을 탐색하면 아래 그림과 같다.
- 탐색을 하면서 시작점으로 부터 거리도 계산한다.
- 정점 u 에 대한 계산
- 시작점으로 부터의 거리 : u.d = 3
- 바로 직전의 정점 (predecessor vertex) : u.π = t
- 직전정점 그래프 Gπ = (Vπ, Eπ)
- 시작점으로 부터 각 정점을 도달하기 직전에 들러야 하는 정점으로 만든 하위 그래프
- Vπ = {v ∈ V:v.π != NIL} U {s}
- Eπ = {(v.π, v): v ∈ Vπ - {s}}
- 그림으로 나타내면 아래와 같다.
- 직전 정점 그래프 Gπ 는 넓이 우선 탐색 트리이다.
- 모든 정점이 연결되어 있고, |Eπ| = |Vπ| - 1 이다.
- 이 때 Eπ 에 포함된 간선을 트리 간선(tree edges)이라고 부른다.
- 정점의 색 구분 (Colors of vertices)
- 초기화한 정점 : 흰색(white) - (not discovered)
- 발견된 정점 : 회색(grayed) - (discovered)
- 완료된 정점 : 검은색(blackened) - (finished)
- 넓이 우선 탐색 (Breadth-first search) Pseudo code
- 1 ~ 7번까지 초기화하는 과정이다.
- 10 ~ 17번까지 넓이 우선으로 탐색하는 과정이다.
- 수행시간 분석
- 초기화 시간 : Θ(V)
- 그래프 탐색 시간 : O(V + E)
- 정점은 최대 한 번만 조사된다.
- 간선은 최대 두 번 조사된다.
- 따라서, 전체 수행시간 : O(V + E)
- 깊이 우선 탐색 (Depth-First search)
- 트리 탐색하는 방법 중에 하나이다.
- 타임 스탬프 (Timestamps)
- 각 정점은 타임 스탬프를 두 개씩 가지고 있다.
- v.d : 발견 시간(discover time)
- v.f : 완료 시간(finishing time)
- 정점의 색 구분(Colors of vertices)
- 초기화한 정점 : 흰색(white) - (not discovered)
- 발견된 정점 : 회색(grayed) - (discovered)
- 완료된 정점 : 검은색(blackened) - (finished)
- 완료의 의미는 인접한 모든 정점을 조사한 경우이다.
- 깊이 우선 탐색 방법은 다음 그림과 같다.
- 알파벳 순으로 깊이 우선 탐색하는 방법이다.
- 위에 언급한 정점의 색 구분으로 탐색한다.
- 탐색의 시작점은 알파벳 중에 가장 먼저 나오는 u 부터 시작한다.
- u 에서 이동 가능한 정점은 v, x 이지만, 알파벳 순이기 때문에 v 먼저 탐색한다.
- 정점 v 에서 이동 가능한 정점은 y 뿐이기 때문에 y 를 탐색한다.
- 정점 y 에서 이동 가능한 정점은 x 뿐이기 때문에 x 를 탐색한다.
- 정점 x 에서는 정점 y 로만 이동 가능하지만 이미 탐색을 했으므로 더 이상 갈 곳이 없다.
- 정점 x 에서는 갈 곳이 없기 때문에 완료 표시를 다음과 같이 해준다.
- 탐색이 끝났으므로 정점 y, v, u 순으로 완료 표시를 해주고 정점 u 에서의 깊이 우선 탐색을 마친다.
- 그 다음 탐색은 탐색이 이루워지지 않은 정점 w 또는 z 를 탐색할 차례이며, 알파벳 순으로 탐색을 하기 때문에 정점 w 부터 탐색한다.
- 정점 w 에서 갈 수 있는 정점은 y, z 로 가능하지만 정점 y 는 이미 탐색이 끝나 완료 되었기 때문에 정점 z 를 탐색한다.
- 정점 z 에서 갈 수 있는 것은 자기 자신이지만 탐색 되었기 때문에 탐색을 종료한다. 조건을 달지 않으면 무한으로 z 를 탐색할 수도 있으니 조심해야한다.
- 정점 z 를 완료한 후에 정점 w 까지 완료한다.
- 깊이 우선 탐색 성능 분석
- 수행시간 분석 : Θ(V + E)
- 넓이 우선 탐색과 깊이 우선 탐색의 차이점
- 넓이 우선 탐색은 거리 기준으로 탐색한다.
- 깊이 우선 탐색은 시간 기준으로 탐색한다.
- 다익스트라 알고리즘
- 다익스트라 알고리즘은 최단 경로를 풀 때 사용되는 알고리즘이다.
- 최단 경로 문제 정의 : 경로에 속하는 모든 간선의 값을 더한 값 중에서 가장 작은 값을 구하는 문제이다. => 가중 경로인 경우는 전체 경로의 합이 가장 작은 값을 구한다.
- 가중 간선(Edge weight) : 간선에 가중치 값이 존재한다.
- 가중 경로(Path weight) : 가중치가 있는 간선의 값을 모두 더한다.
- 최단 경로 예시) 정점 u 에서 v 까지의 최단 경로
- 정점 u 에서 정점 v 까지의 경로 중에 경로의 값이 가장 작은 경로
- 정점 u 를 시작점(source) 이라고 하고, 정점 v 도착점(destination) 이라고 한다.
- 정점 u 에서 v 까지의 최단 경로 값 : δ(u, v)
- 최단 경로 문제의 구분 : 시작점(source)과 도착점(destination)의 수에 따라 다음과 같이 구분
- Single-source & Single-destination (시작점 1 : 도착점 1)
- Single-source (시작점 1 : 도착점 n)
- Single-destination (시작점 n : 도착점 1)
- All pairs (시작점 n : 도착점 m)
- 시작점과 도착점의 수에 따라서 문제의 난이도가 어려워지는 것이 아니고 단지 수행횟수가 증가하게 되는 것이다.
- 시작점이 1개이고, 도착점도 1개이면, 수행횟수가 1번이라고 보면 시작점이 1개 이고 도착점이 n개 이면, 시작점, 도착점 모두 1개 일 때의 수행횟수를 n개로 하는 것이고, 나머지도 동일하게 보면 된다.
- 다익스트라 알고리즘(Dijkstra's algorithm)
- 하나의 시작점(source)에서 하나의 도착점(destination)을 가는 최단경로를 찾는 알고리즘
- 간선이 음의 값을 가져서는 안된다.(non-negative edges only)
- 다익스트라 알고리즘 Pseudo code
- 다익스트라 알고리즘의 수행과정
- 시작점을 기준으로 갈 수 있는 정점을 찾고, 갈 수 있는 간선에 포함되는 정점에 간선의 가중치 값을 표시 후에 가장 작은 가중치를 갖는 간선의 정점을 선택한다.
- 선택한 정점을 기준으로 갈 수 있는 간선의 가중치를 현재 가중치에 더한 후에 다음 정점에 표시하고 그 중에서 다른 경로의 가중치보다 더 작은 값을 가지는 지 Relax 작업을 진행한다.
- 1,2 번의 과정을 시작점에서 모든 정점이 다 탐색이 될 때까지 진행한다.
- 다익스트라 알고리즘의 수행시간 분석
- 배열로 구현한 경우 : O(V^2)
- 힙구조로 구현한 경우 : O(Vlog(V) + Elog(V))
- 피보나치 힙으로 구현한 경우 : O(Vlog(V) + E)
- 벨만-포드 알고리즘
- 벨만-포드 알고리즘도 다익스트라 알고리즘과 마찬가지로 최단 경로를 푸는 알고리즘이다.
- 최단경로 문제
- 정의(Definition)
- 정점 u 에서 v 까지의 최단 경로
- 정점 u 에서 정점 v 까지의 경로 중에 경로의 값이 가장 작은 경로
- 정점 u 를 시작점이라고 하고, 정점 v 를 도착점이라고 한다.
- 정점 u 에서 v 까지의 최단 경로 값 : δ(u, v)
- 구분
- Single-source & Single-destination (시작점 1 : 도착점 1)
- Single-source (시작점 1 : 도착점 n)
- Single-destination (시작점 n : 도착점 1)
- All pairs (시작점 n : 도착점 m)
- 벨만-포드 알고리즘(The Bellman-Ford algorithm)
- 다익스트라 알고리즘에서는 음수 간선 값에 대해서는 다루지 않았으나 벨만-포드 알고리즘에서는 음수 간선 값도 포함해서 최단 경로를 구한다.
- 벨만-포드 알고리즘에서는 음의 값을 가지는 간선 값이 있는 경우가 문제가 되는 것이 아닌 음의 값을 가지는 간선이 순환하는 경우에 문제가 되는데 이 때, 벨만-포드 알고리즘에서는 출발점으로부터 도달 가능하며 음의 값을 가지는 순환이 없는 경우로 생각한다.
- 최단 경로는 순환을 포함해서는 안된다.
- 최단 경로의 길이는 최대 |V|-1 이다.
- 벨만-포드 알고리즘 Pseudo code
- 벨만-포드 알고리즘 수행
- 시작점을 중심으로 갈 수 있는 정점을 이동한 다음에 Relax 작업한다.
- 완화 작업(Relax) : 현재 경로 값보다 더 작은 경로가 존재한다면 값을 변경한다.
- 한 번 간선을 탐색하고 Relax 작업으로 더 작은 경로가 있는지 확인하면서 계속 진행한다.
- 벨만-포드 알고리즘의 수행시간 : O(VE)
- 플로이드-와샬 알고리즘
- 플로이드-와샬 알고리즘은 All pairs (시작점 n : 도착점 m) 에 관련해서 최단 경로를 찾는 알고리즘이다.
- 최단 경로 문제
- 정의(Definition)
- 정점 u 에서 v 까지의 최단 경로
- 정점 u 에서 정점 v 까지의 경로 중에 경로의 값이 가장 작은 경로
- 정점 u 를 시작점이라고 하고, 정점 v 를 도착점이라고 한다.
- 정점 u 에서 v 까지의 최단 경로 값 : δ(u, v)
- 구분
- Single-source & Single-destination (시작점 1 : 도착점 1)
- Single-source (시작점 1 : 도착점 n)
- Single-destination (시작점 n : 도착점 1)
- All pairs (시작점 n : 도착점 m)
- 플로이드-와샬 알고리즘(Floyd-Warshall algorithm)
- 플로이드-와샬 알고리즘은 All pairs 에 대해서 인접행렬을 이용해서 최단 경로 문제를 해결하는 알고리즘이다.
- 인접행렬 W
- 각 정점에서 바로 연결 가능한 간선에 해당하는 정점을 표시한다.
- 각 간선의 값은 다음과 같이 표시한다 : w(ij) = w(i, j)
- 최단 경로 행렬 D
- 모든 시작점, 도착점에 대해서 가장 짧은 최단 경로 행렬을 표시한다.
- 각 경로의 값은 다음과 같이 표시한다 : d(ij) = δ(u, v)
- 직전 정점 행렬 π
- 최단 경로를 가기 위해서 직전에 탐색하는 정점을 표시한다.
- 각 행렬의 값은 다음과 같이 표시한다.
- 정점 i 와 정점 j 사이에 경로가 존재하지 않으면 π(ij) = NIL
- π(ij) 는 정점 j 의 직전 정점이다.
- 각 행렬의 값은 다음과 같이 표시한다.
- 모든 정점에 대한 최단 경로 출력하는 Pseudo code
- 중간 정점 : 단순 경로 <v1, v2, ... , vl>가 있다고 할 때, v1 과 vl 사이에 있는 정점을 중간 정점이라고 한다.
- 최단 경로의 구성
- 플로이드-와샬 알고리즘은 중간 정점을 모두 실험해본다.
- 정점 집합이 V = {1, 2, ... , n} 이라고 하면, i, j ∈ V 일 때, i 와 j 사이에 정점 집합 V 에 속하는 모든 정점을 넣어보고 경로의 값이 가장 작아지는 경로를 찾는다.
- 따라서 수행시간은 Θ(V^3)
- 재귀해법
- 정점 i 부터 j 까지 최단 경로를 d(ij)^k 이라고 하자.
- 이 때 {1, 2, ... , k} 은 중간 정점의 집합니다.
- 다음과 같은 재귀식을 구할 수 있다.
- 플로이드-와샬 알고리즘 Pseudo code
- 수행과정
- 각 정점에 대한 인접행렬을 구성한다. 이 때, 갈 수 없는 정점은 무한대로 표시한다.
- 각 정점의 최단 경로 행렬 D 를 구성하고, 직전 정점 행렬 π 를 구성한다.
- 위의 정점이 1 부터 5 까지 존재하므로 각 정점에 대한 최단 경로 행렬 D 와 직전 정점 행렬 π 를 구성한다.
- 구성 시에 직전 정점 행렬에서 직전에 가는 것이 없다면, NIL 로 표시한다.
- 탐욕 알고리즘
- 탐욕 알고리즘이란?
- 탐욕 알고리즘은 최단 경로를 찾거나 기타 다른 해결 방법을 찾을 때, 현재 상황에서 가장 좋아 보이는 답을 선택하는 방법이다.
- 각 부분에서 최적을 선택하면 전체에서도 최적이 될 것이라는 가정을 전제로 한다.
- 선택은 항상 하위 문제에 대한 해답이 나오기 전에 선택된다.
- 탐욕 알고리즘과 동적 프로그래밍의 차이점
- 탐욕 알고리즘(Greedy-choice property)
- 하위 문제를 풀기 전에 선택을 한다.
- 항상 하나의 문제만을 고려한다.
- 동적 프로그래밍(Dynamic programming)
- 하위 문제를 풀고나서 선택을 한다.
- 동시에 여러 개의 하위 문제를 고려한다.
- 가중 무방향성 그래프(Weighted undirected graph)
- G = (V, E)
- 간선 집합에 속하는 각 간선(u, v) 는 w(u, v)을 가진다.
- 신장트리(Spanning Trees)
- 그래프 G의 신장트리 (A spanning tree for G)
- 트리가 그래프 G의 모든 정점을 포함할 때 그래프 G에 속하는 트리의 간선을 선택한 것이다.
- 최소 신장트리(Minimum Spanning Trees)
- 신장트리의 비용(Cost of a spanning tree)
- 최소 신장 트리 문제 : 비용이 최소가 되는 신장트리를 찾는 문제
- 일반적인 MST Pseudo code
- 최소 신장 트리는 한번에 하나의 간선이 늘어난다.
- 간선(u, v)을 집합 A에 추가하고, A U {(u, v)} 가 최소 신장트리의 일부가 되는지 확인한다. 이 때, 이런 간선을 안전 간선(safe edge) 이라고 한다.
- 프림 알고리즘(Prim's Algorithm)
- 집합 A에 속하는 간선은 항상 트리를 형성한다.
- 트리는 임의의 root 정점 r에서 시작하며 정점의 집합 V 에 속하는 모든 정점을 포함할 때까지 확장한다.
- 각 단계에서 가벼운 간선(light edge) 이 트리에 추가된다.
- 따라서, 알고리즘이 종료되면, 최소 신장 트리가 만들어진다.
- 프림 알고리즘 Pseudo code
- 프림 알고리즘 과정
- 알파벳 순을 기준으로 다음 그래프를 프림 알고리즘으로 최소 신장 트리를 만든다고 하면, 가장 먼저 정점 a 부터 시작한다.
- 정점 a 에서 가장 가중치가 작은 간선을 선택하면 정점 b 와 연결해준다.
- 다음의 과정을 그 다음 정점에 이어서 선택 가능한 간선 중에 작은 간선들을 선택하면서 트리를 만족해야 되니 연결을 했을 때 Cycle 이 되지 않도록 정점을 연결하다보면 아래와 같은 그림이 된다.
- 프림 알고리즘은 cut 으로 무방향성 그래프에서 정점을 두개로 나눈 집합으로 생각한다.
- 간선 (u, v)의 끝점이 하나는 S 에 있고, 다른 하나는 V-S 에 있는 경우 간선(u, v) 가 cut(S, V-S) 을 가로지른다(cross) 라고 한다.
- 만약 A 에 속한 어떤 간선도 cut 을 가로지르지 않으면, cut 이 A 를 보장한다.
- 만약 어떤 간선의 값이 cut 을 가로지르는 간선 중에 가장 작다면 그 간선을 가벼운 간선(light edge) 라고 한다.
- 쿠루스칼 알고리즘(Kruskal's Algorithm)
- 쿠르스칼 알고리즘은 정점이 아닌 간선을 중심으로 작은 값들을 이어서 최소 신장 트리를 만든다.
- 이 때, Cycle 이 발생하지 않도록 정점을 연결한다.
- 쿠르스칼 알고리즘 Pseudo code
- 쿠루스칼 알고리즘 과정
- 동일한 그래프를 정점이 아닌 간선을 기준으로 작은 값부터 하나씩 연결해간다. 알파벳을 기준으로 아래 그림에서 가장 작은 간선의 값은 정점 h 와 정점 g 를 잇는 간선이므로 가장 먼저 연결한다.
- 그 후에 그 다음으로 큰 간선을 찾아서 연결을 하며, 같은 간선의 값이 있으며, 연결 후에 Cycle 이 되지 않는다면, 모두 연결한다.
- 동일한 방법으로 모든 간선을 모두 연결해보는 과정을 거치며, Cycle 이 발생하지 않도록 하며 다음과 같이 최소 신장 트리를 구성한다.
- 탐욕 알고리즘은 현재에서 최선인 방법을 찾는 알고리즘으로 최단 경로의 최소 신장 트리를 구성하는 방법으로 정점을 기준으로 하는 프림 알고리즘과 간선을 기준으로 하는 쿠루스칼 알고리즘이 있다.
| INSERTION-SORT(A) for j = 2 to A.length key = A[j] i = j - 1 while i > 0 and A[i] > key A[i + 1] = A[i] i = i - 1 A[i + 1] = key |
|---|
| INSERTION-SORT(A) | cost | times |
|---|---|---|
| for j = 2 to A.length | c1 | n |
| key = A[j] | c2 | n-1 |
| i = j - 1 | c3 | n-1 |
| while i > 0 and A[i] > key | c4 | n ∑tj j=2 |
| A[i + 1] = A[i] | c5 | n ∑(tj-1) j=2 |
| i = i - 1 | c6 | n ∑(tj-1) j=2 |
| A[i + 1] = key | c7 | n-1 |
| MERGE-SORT(A, p, r) if p < r q = [(p + r)/2] MERGE-SORT(A, p, q) MERGE-SORT(A, q + 1, r) MERGE(A, p, q, r) |
|---|
| BUILD-MAX-HEAP(A) A.heap-size = A.length for i = [A.length/2] downto 1 MAX-HEAPIFY(A, i) |
|---|
| HEAPSORT(A) for i = [A.length / 2] downto 2 exchange A[1] with A[i] A.heap-size = A.heap-size-1 MAX-HEAPIFY(A, i) |
|---|
| QUICKSORT(A, p, r) if p < r q = PARTITION(A, p, r) QUICKSORT(A, p, q - 1) QUICKSORT(A, q + 1, r) |
|---|
| DIRECT-ADDRESS-SEARCH(T, k) return T[k] DIRECT-ADDRESS-INSERT(T, x) return T[x.key] = x DIRECT-ADDRESS-DELETE(T, x) return T[x.key] = NIL |
|---|
| CHAINED-HASH-INSERT(T, x) insert x into list T[h(x.key)] CHAINED-HASH-DELETE(T, x) delete x from the list T[h(x.key)] CHANINED-HASH-SEARCH(T, x) search for an element with key k in list T[h(k)] |
|---|
| HASH-INSERT(T, k) i = 0 repeat j = h (k, i) if T [ j] == NIL T [ j] = k return j else i = i +1 until i == m error “hash table overflow” |
|---|
| HASH-SEARCH(T, k) i = 0 repeat j = h (k, i) if T [ j] == k return j i = i +1 until T [ j] == NIL or i == m return NIL |
|---|
| BFS(G, s) 1 for each vertex u ∈ G.V - {s} 2 u.color = WHITE 3 u.d = ∞ 4 u.π = NIL 5 s.color = GRAY 6 s.d = 0 7 s.π = NIL 8 Q = Ø 9 ENQUEUE(Q, s) 10 while Q != Ø 11 u = DEQUEUE(Q) 12 for each v ∈ G.Adj[u] 13 if v.color == WHITE 14 v.color = GRAY 15 v.d = u.d + 1 16 v.π = u 17 ENQUEUE(Q, v) 18 u.color = BLACK |
|---|
| DIJKSTRA(G, w, s) INITIALIZE-SINGLE-SOURCE(G, s) S ← Ø Q ← V[G] while Q != Ø do u ← EXTRACT-MIN(Q) S ← S ∈ {u} for each vertex v ∈ Adj[u] do RELAX(u, v, w) |
|---|
| BELLMAN-FORD(G, w, s) INITIALIZE-SINGLE-SOURCE(G, s) For i ← 1 to |V[G]|-1 do for each edge(u,v) ∈ E[G] do RELAX(u, v, w) for each edge(u,v) ∈ E[G] do if d[v] > d[u] + w(u, v) then return FALSE return TRUE |
|---|
| PRINT-ALL-PAIRS-SHORTEST-PATH(π, i, j) 1 if i = j 2 then print i 3 else if π(i,j) = NIL 4 then print"no path from" i "to" j "exists" 5 PRINT-ALL-PAIRS-SHORTEST-PATH(π, i, π(i,j)) 6 print j |
|---|
| FLOYD-WARSHALL(W) 1 n ← rows[W] 2 D(0) ← W 3 for k ← 1 to n 4 do for i ← 1 to n 5 do for j ← 1 to n 6 do d(ij)^k ← min(d(ij)^(k-1), d(ik)^(k-1)+d(kj)^(k-1)) 7 return D(n) |
|---|
| GENERIC-MST(G, W) 1 A ← Ø 2 while A does not form a spanning tree 3 do find an edge (u, v) that is safe for A 4 A ← A U {(u, v)} 5 return A |
|---|
| MST-PRIM(G, W, r) 1 for each u ∈ V[G] 2 do key[u] ← ∞ 3 π[u] ← NIL 4 key[r] ← 0 5 Q ← V [G] 6 while Q != Ø 7 do u ← EXTRACT-MIN(Q) 8 for each v∈Adj[u] 9 do if v ∈ Q and w(u, v) < key[v] 10 then π[v] ← u 11 key[v] ← w(u, v) |
|---|
| MST-KRUSKAL(G, W) 1 A ← Ø 2 for each vertex v ∈ V[G] 3 do MAKE-SET(v) 4 sort the edges of E into nondecreasing order by weight w 5 for each edge (u, v) ∈ E, taken in nondecreasing order by weight 6 do if FIND-SET(u) ≠ FIND-SET(v) 7 then A ← A ∪ {(u, v)} 8 UNION(u, v) 9 return A |
|---|